A quick learning about Identity function and squared function

1. Exploring the Identity Function

The identity function is one of the simplest functions in mathematics. It is defined as: f(x) = x

Graph Overview:

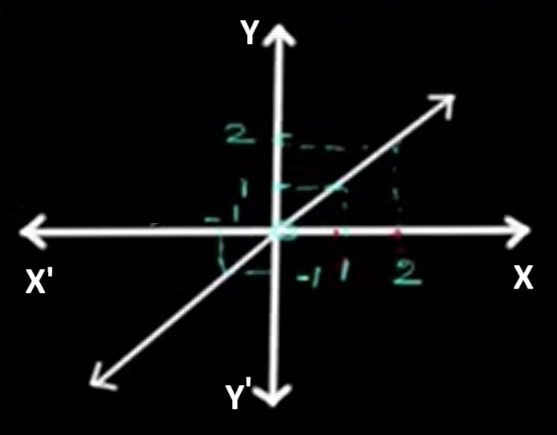
The graph of the identity function is a straight line passing through the origin, with a slope of 1. Every point on the graph has coordinates where the input equals the output, such as (1,1), (2,2), and so on.

Domain:

The function is defined for all real numbers. Domain: (-∞, ∞)

Range:

The output also includes all real numbers. Range: (-∞, ∞)

Key Characteristics:

• It passes through the origin (0,0).
• Slope is 1, meaning a 45° angle from the x-axis.
• Every input equals its output.

2. Exploring the Squared Function

The squared function, also called the parabola function, is written as: f(x) = x²

Graph Overview:

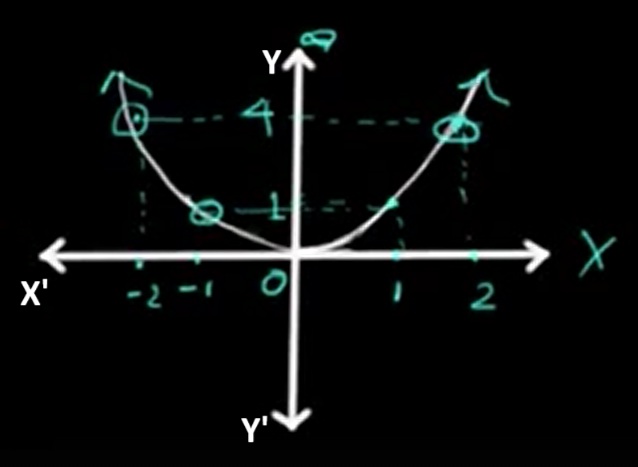
The graph of this function is a U-shaped curve called a parabola. It is symmetric about the y-axis and opens upwards. As x moves away from 0, the y-values increase rapidly.

Domain:

The function accepts all real numbers as input. Domain: (-∞, ∞)

Range:

Since squaring any real number results in a non-negative output, the function never produces negative values. Range: [0, ∞)

Key Characteristics:

• The graph is symmetric with respect to the y-axis.
• It passes through the point (0, 0), which is its minimum.
• The rate of increase becomes steeper as x increases or decreases away from 0.

Conclusion

The identity and squared functions offer a foundation for understanding more complex mathematical concepts. The identity function represents direct proportionality, while the squared function introduces the idea of nonlinear growth. Studying their graphs helps learners visually grasp their unique behaviors.