A quick learning of Modulus and Greatest integer function through Graph

1. Understanding the Modulus Function

The modulus function, often known as the absolute value function, is represented by f(x) = |x|. No matter if x is positive or negative, the output is always a non-negative number.

Graph Overview:

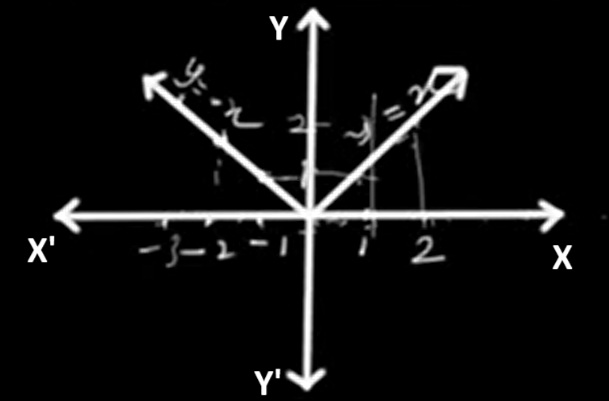
The graph of f(x) = |x| creates a V-like pattern on the coordinate plane. It is symmetric about the y-axis and increases in both directions from the origin.

Domain:

You can use any real number as input for this function. Domain: (-∞, ∞)

Range:

Since the output is never negative, all values are zero or greater. Range: [0, ∞)

Key Points to Remember:

• f(-3) = 3
• f(0) = 0
• f(4) = 4

2. Exploring the Greatest Integer Function

The greatest integer function is denoted by f(x) = ⌊x⌋. It gives the largest whole number that is less than or equal to the input x.

Graph Overview:

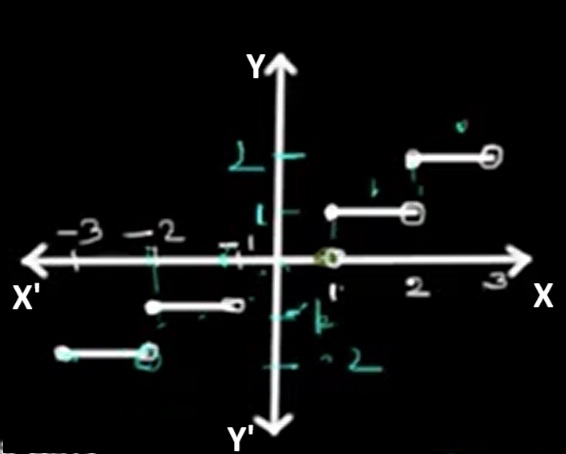
The graph of this function appears as a staircase, known as a step function. Each step is flat, beginning at an integer and ending just before the next one. The function value matches the starting integer of each interval.

Domain:

All real numbers can be used as input for this function. Domain: (-∞, ∞)

Range:

Only integers appear as outputs of the function. Range: {..., -2, -1, 0, 1, 2, ...}

Key Points to Remember:

• f(2.9) = 2
• f(-1.1) = -2
• f(3) = 3

Conclusion

Graphs are a powerful tool for quickly understanding how functions behave. The modulus function forms a simple V-shape, showing how it turns negatives into positives. Meanwhile, the greatest integer function's step-like structure clearly illustrates how values are rounded down to the nearest whole number.

With practice, identifying the domain, range, and graph of these functions becomes intuitive and helps build a strong foundation in algebra.