In this lesson, we explore the geometric meaning of the cross product (also called the vector product) of two vectors A and B. Consider the diagram below, where point O is taken as the origin of reference. Along OA and OB, we define vectors \( \vec{a} \) and \( \vec{b} \) respectively.
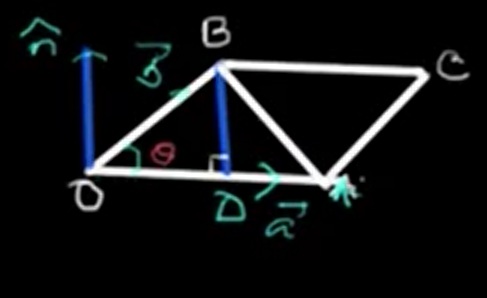
We know that when we compute the cross product \( \vec{a} \times \vec{b} \), the resulting vector is perpendicular to the plane formed by \( \vec{a} \) and \( \vec{b} \). The blue line in the diagram represents the perpendicular vector at the origin O.
Imagine drawing a line BD that stands perpendicular to both vectors \( \vec{a} \) and \( \vec{b} \), pointing in the same direction as their cross product \( \vec{a} \times \vec{b} \). The quadrilateral OACB forms a parallelogram where OA and OB are adjacent sides.
The standard formula used to determine the area of a parallelogram is:
\[ Area\; of\; parallelogram = Base \times corresponding\; altitude = OA \times BD \]
From the right triangle formed, we get:
\[ \frac{BD}{OB} = \sin \theta \quad \Rightarrow \quad BD = OB \sin \theta = |\vec{b}| \sin \theta \]
By inserting this expression into the area formula, we obtain:
\[ Area\; of\; the\; parallelogram = |\vec{a}| \cdot |\vec{b}| \sin \theta \; ...(1) \]
According to the definition of the cross product's magnitude:
\[ |\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \sin \theta \;...(2) \]
By comparing equations (1) and (2), we find that:
\[ |\vec{a} \times \vec{b}| = \;Area\; of\; the\; parallelogram\; formed\; by\; \vec{a} \; and\; \vec{b} \]
Lastly, the area of \(\triangle\) OAB—being half of the parallelogram OACB—can be calculated as:
\[ Area\; of\; \triangle OAB = \frac{1}{2} Area\; of\; parallelogram \; OACB \] nbsp;nbsp;nbsp; nbsp; \[ =\frac{1}{2} |\vec{a} \times \vec{b}| \]