Ten Standard >> Area and perimeter of sector of a circle

Perimeter, area of a sector

What is a sector?

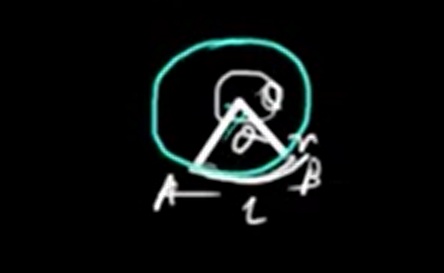
A sector is a part of the area of a circle. \(\tt \theta\) is angle subtends by the arc. Using \(\tt \theta\) we can find the length of the arc. Length of the arc AB=l. The length of the arc is part of the circumference. When the length of the arc is AB it subtends angle \(\tt \theta\) at the centre. And when we consider the whole circumference the angle subtended at the centre is \(\tt 360^{o}\).   

So we can write that

  \(\tt \frac{l}{\theta}=\frac{2 \pi r}{360^{o}}\)
\(\tt \Rightarrow\ l=\frac{\theta}{360^{o}} \times 2 \pi r\)

i) length of arc AB=\(\tt \frac{\theta}{360^{o}} \times 2 \pi r\)
                   =\(\tt \frac{\theta}{180^{o}} \times \pi r\) unit

ii) perimeter of sector AOB=OA+ arc AB+ BO
                                 =\(\tt r+ \frac{\theta}{360^{o}} \times 2 \pi r +r\)
                                 =\(\tt 2r+ \frac{\theta}{360^{o}} \times 2 \pi r \) unit

iii) Area of the sector AOB:

    \(\tt \frac{Sector\ AOB}{area\ of\ the\ whole\ circle}=\frac{\theta}{360^{o}}\) 

\(\tt \therefore\ AOB=\frac{\theta}{360^{o}} \times area\ of\ the\ whole\ circle\)
                =\(\tt \frac{\theta}{360^{o}} \times \pi r^{2}\) sq units

Special cases:

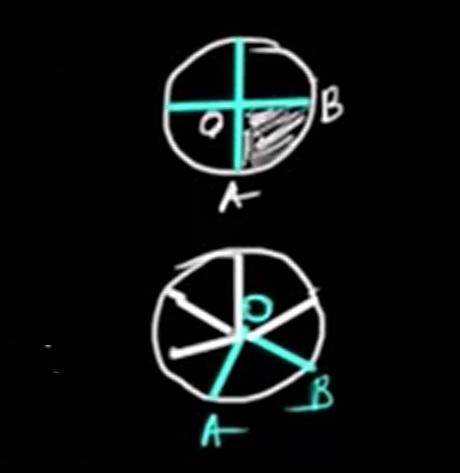
1) Quadrant=\(\tt \frac{1}{4} of \the\ whole\ circle\)
   \(\tt \therefore\ area\ of \the\ quadrant\ AOB=\frac{1}{4} \pi r^{2}\) sq units

2) \(\tt \angle AOB=60^{o}\),
     when \(\tt \theta=60^{o}\), circle is divided into 6 equal parts
   \(\tt \therefore\ each\ part=\frac{1}{6} \pi r^{2}\) sq units

3) \(\tt \angle AOB=30^{o}\),
     when \(\tt \theta=30^{o}\), circle is divided into 12 equal parts
   \(\tt \therefore\ each\ part=\frac{1}{12} \pi r^{2}\) sq units

4) \(\tt \angle AOB=120^{o}\),
     when \(\tt \theta=120^{o}\), circle is divided into 3 equal parts
   \(\tt \therefore\ each\ part=\frac{1}{3} \pi r^{2}\) sq units