Twelve Standard >> Composition of functions | Introduction

Introduction of Composite function

A composite function is a composition of two or more functions.

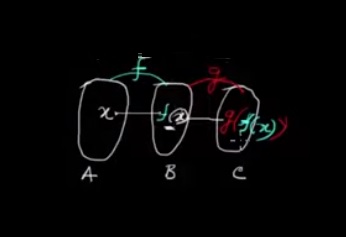
Let A, B and C are three nonempty sets such that f:A \(\rightarrow\) B and g:B\(\rightarrow\) C . 
So here the codomain of function f is domain of function g happens then only we can define
gof(x)=g(f(x))        

Illustration 1: Let f:{2, 3, 4, 5} \(\rightarrow\) {3, 4, 5, 9} and g: {3, 4, 5, 9} \(\rightarrow\) {7, 11, 15} be defineal as f(2)=3, f(3)=4, f(4)=f(5)=5 and g(3)=g(4)=7 and g(5)=g(9)=11, find gof.

Solution:    

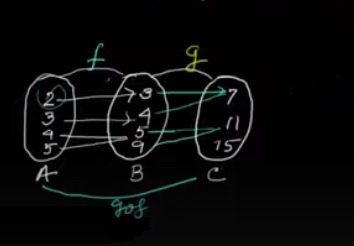
    gof(2)=g(3)=7
    gof(3)=g(4)=7
    gof(4)=g(5)=11
    gof(5)=g(5)=11

Illustration 2: Let R be the set of real number. Define function f:R \(\rightarrow\)  R by f(x)=\(8x^{3}\) and g:R \(\rightarrow\) R by g(x)=\(\sqrt[3]{x}\), find fog(x) and gof(x).

Solution:

As f:R\(\rightarrow\) R, 
    g:R\(\rightarrow\) R,
  fog & gof can e defined.

fog(x)=f(g(x))=8\((g(x))^{3}\)
         = 8 \((\sqrt[3]{x})^{3}\)
         =8\(.x^{\frac{1}{3} \times 3}\)=8x

gof(x)=g(f(x))=\(\sqrt[3]{8x^{3}}\)
          =2x