Example 1: Draw the graph of the equations x-2y=9 and 6y=3x+21
Solution:
x-2y=9
\(\Rightarrow \) 2y=x-9
\(\Rightarrow \) y=\(\frac{x-9}{2} \)...(1)
6y=3x+21
\(\Rightarrow \) y=\(\frac{3x+21}{6} \)...(2)
from relation (1),
| x | 1 | 3 | 5 |
| y | -4 | -3 | -2 |
So from relation (1) we get points (1, -4), (3, -3), and (5, -2)
from relation (2),
| x | 1 | 3 | 5 |
| y | 4 | 5 | 6 |
So from equation (1) we get points (1, 4), (3, 5), and (5, 6)
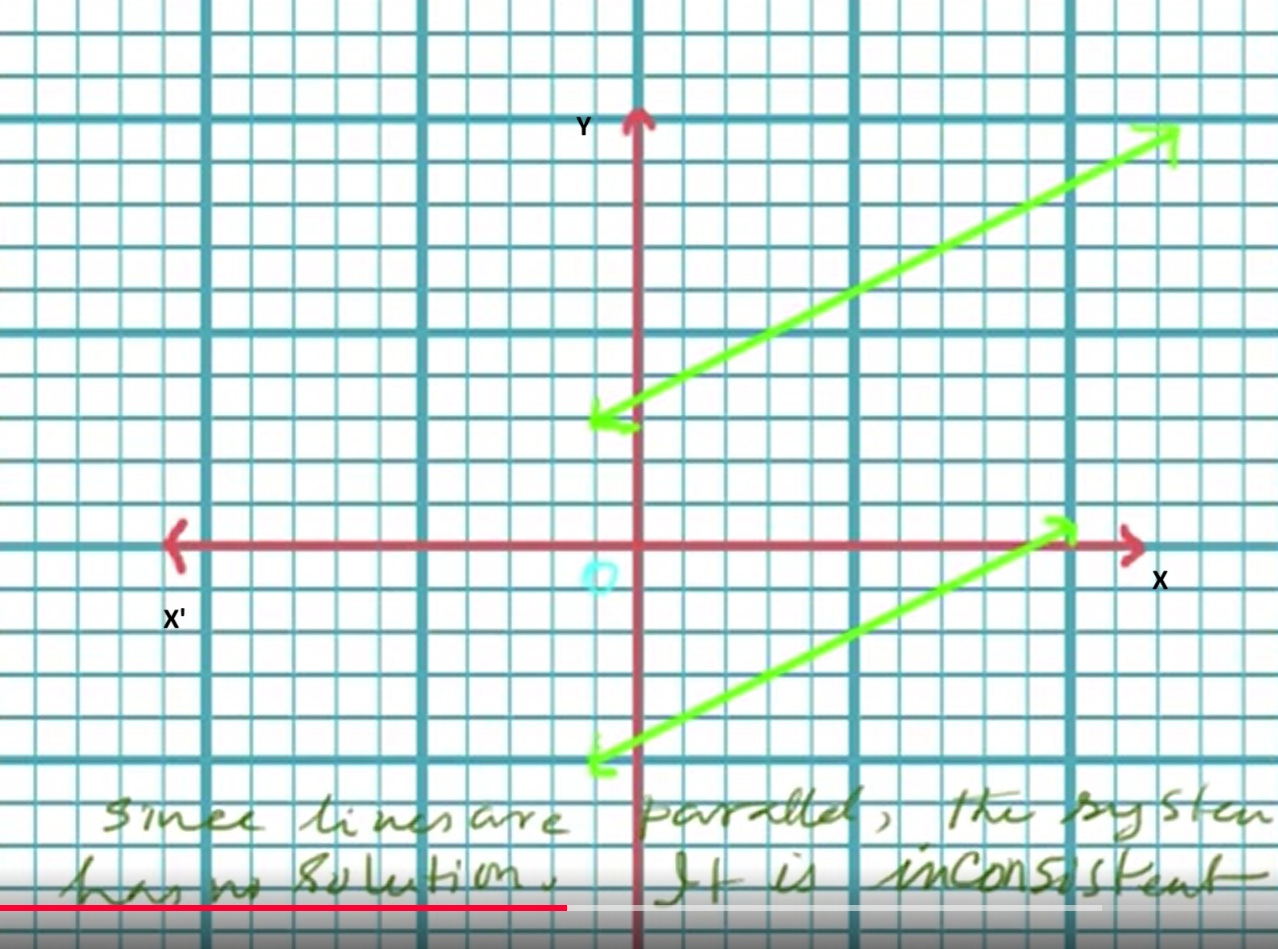
Look at the image above. Since lines are parallel, the system has no solution. It is inconsistent.