Ten Standard >> Graphical solution of a pair of linear equations | Introduction

Graphical solution of a daily life situation

\(a_{1}x+b_{1}y+c_{1}=0\), \(a_{2}x+b_{2}y+c_{2}=0\) are two linear simultaneous linear equation in two variable x and y. 

If graphs are drawn with these equations then three cases can arise

i) Two lines are meat at a point, the system has a unique solution.

ii) If two lines are parallel, there is no solution. The system is inconsistent.

iii) If two lines overlap each other, there are infinitely on any solution.

Example: 1 pencil and 5 pens together cost Rs 26 whereas 5 pencils and 4 pens together cost also Rs 26. Frame this situation algebraically and solve it geometrically to get the cost price of 1 pencil and 1 pen.

Solution: Let the cost of 1 pencil is Rs x
                    cost of 1 pen is Rs y

     3x+5y=26
     \(\Rightarrow\) y=\(\frac{26-3x}{5}\)...(1)
     5x+4y=26
     \(\Rightarrow\) y=\(\frac{26-5x}{4}\)...(2)

from relation (1),       

So from relation (1) we get points (2, 4), (7, 1), and  (-3, 7)

from relation (2),  

So from relation (2) we get points (2, 4), (6, -1) and  (-2, 9)

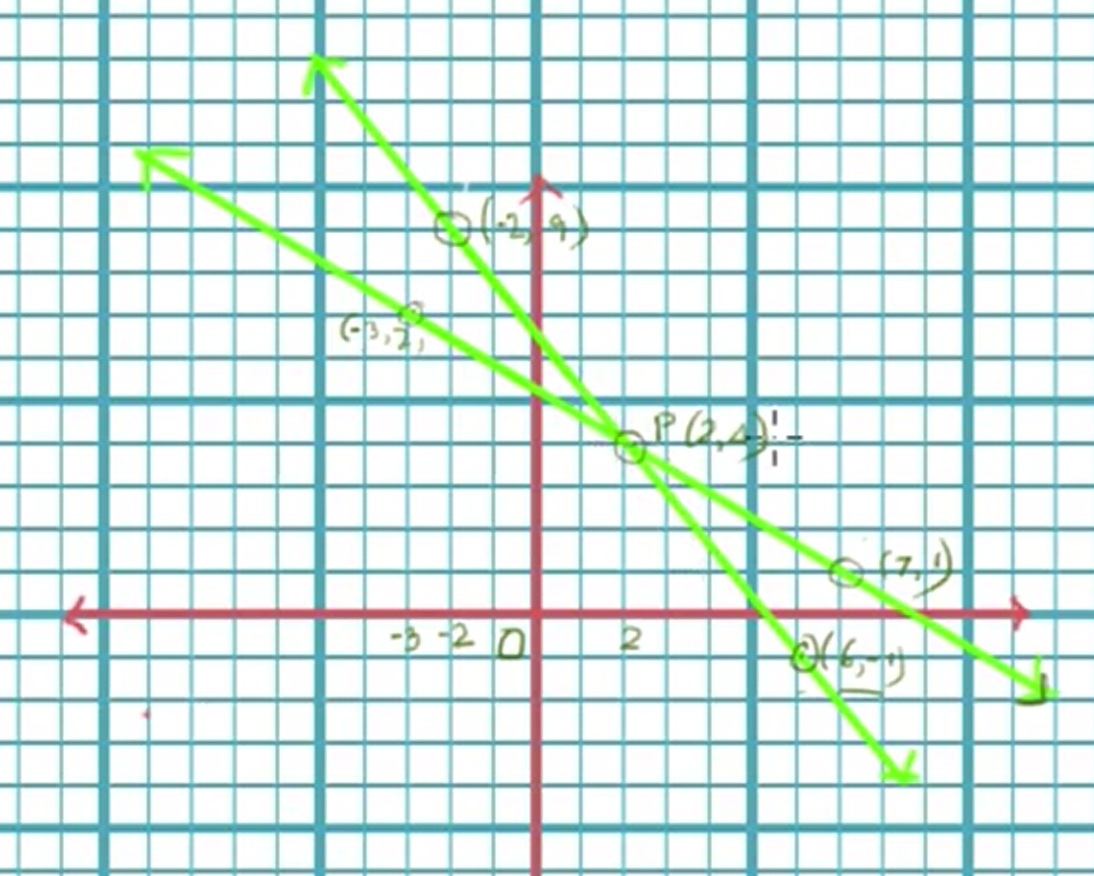
From the graph, we see that two lines intersect at (2, 4). So the solution is x=2 and y=4
We get other information that

The cost price of 1 pencil = Rs 2
The cost price of 1 pen = Rs 4