REAL NUMBERS | Irrational Numbers | Part -5

How to Plot \( \sqrt{2} \) on the Number Line Using Geometry

The square root of 2 (\( \sqrt{2} \)) is an irrational number, meaning it cannot be exactly represented as a fraction. However, we can geometrically represent it using basic constructions involving a number line, a semicircle, and right triangle geometry.

Construction Steps

1. Draw a horizontal line and mark a point A.
2. From point A, mark point B such that AB = 1 unit.
3. Continue the line beyond point B and place point C such that the segment BC measures exactly 1 unit.
4. This gives the entire segment AC = AB + BC = 2 units.
5. Find the midpoint O of segment AC. So AO = OC = 1 unit.
6. Using O as the center and OA (or OC) as the radius, draw a semicircle passing through points A and C.
7. At point B (the point between A and C), draw a perpendicular line upward that intersects the semicircle at point D.
8. Join points D and B. The triangle ΔODB forms a right-angled triangle, as it is inscribed within a semicircle.

Why This Represents \( \sqrt{2} \)

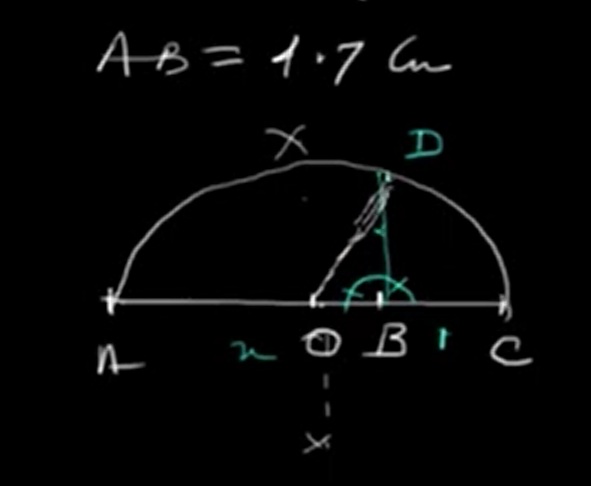
From the construction:

• AB = 1 unit
• BC = 1 unit
• AC = 2 units
• O is the midpoint of AC, so AO = OC = 1

Triangle ODB is a right triangle, as any angle formed within a semicircle is a right angle, according to the semicircle property.

Using Pythagoras Theorem in Triangle ODB:

In triangle ODB:
- OB is the base = distance from O to B = \( OC - BC = 1 - 1 = 0 \) → (Corrected below)
Since point B is located between A and C, with both segments AB and BC measuring 1 unit each, the total distances can be described as:

• AC = 2 units
• O is the midpoint → OC = AO = 1
• OB = distance from midpoint O to B = \( OC - 1 = 1 - 1 = 0 \)? (Incorrect — Let’s fix this)

Assuming point A is at 0, and since B is 1 unit away from A while O is the midpoint of segment AC, the coordinates can be assigned as follows:

• A = 0
• B = 1
• C = 2
• O = midpoint of A and C = (0 + 2)/2 = 1
• So B and O are at the same point ⇒ this construction wouldn't work for \( \sqrt{2} \)

Corrected Construction for \( \sqrt{2} \)

1. Let AB = 1 unit
2. Construct a perpendicular line at B
3. Mark a point D on the perpendicular such that BD = 1 unit
4. Join A to D to form triangle ΔADB

Now, in right triangle ADB, by the Pythagorean theorem: \( AD^2 = AB^2 + BD^2 = 1^2 + 1^2 = 2 \) \( \Rightarrow AD = \sqrt{2} \)

This line segment AD represents \( \sqrt{2} \). You can now use a compass to transfer this length from A onto the number line to geometrically mark \( \sqrt{2} \).

Conclusion

The square root of 2 can be constructed using basic geometric tools and the Pythagorean theorem. Such constructions visually demonstrate that irrational numbers like \( \sqrt{2} \) have a precise location on the real number line, even though they cannot be written as exact fractions.