A prism is a three-dimensional solid object with two identical and parallel polygonal faces (called bases) and other faces that are parallelograms. These parallelogram faces connect corresponding sides of the two bases.
In geometry, a prism is defined as a polyhedron with two congruent polygonal bases and all other faces (called lateral faces) being parallelograms. The height of the prism is the perpendicular distance between the two bases.
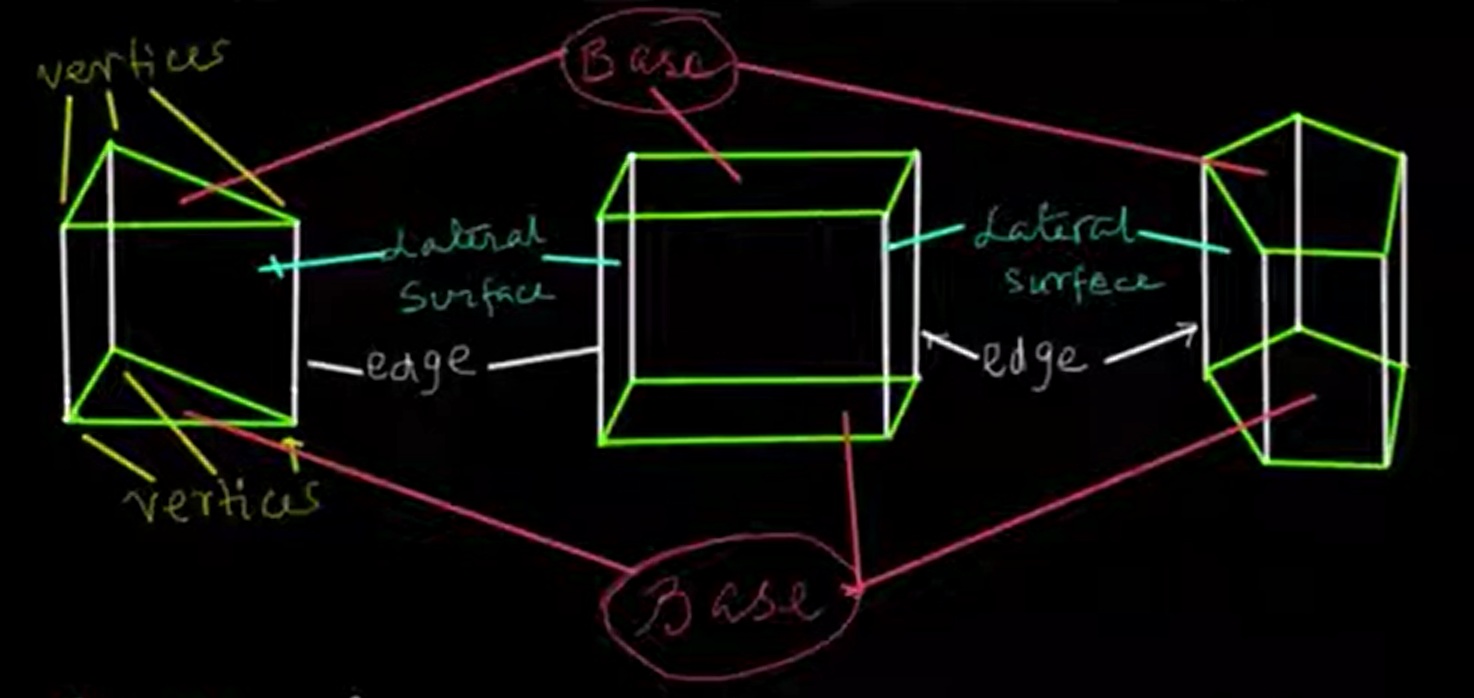
The shape of the base determines the name of the prism. For example:
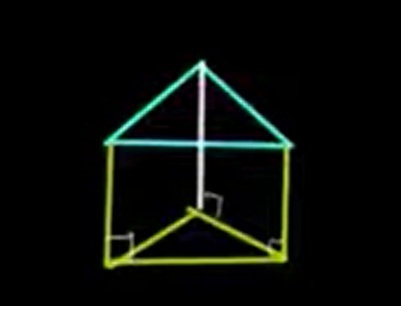
A right prism is a prism in which the lateral edges (sides) are perpendicular to the bases. This means all the lateral faces are rectangles. The sides do not lean or slant.

An oblique prism has lateral edges that are not perpendicular to the bases. In this case, the sides are parallelograms that slant between the bases, and the prism appears "tilted."
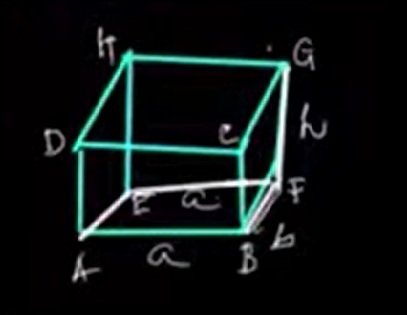
A rectangular prism is a right prism with rectangular bases and rectangular lateral faces. If the prism has:
The surface area \( A \) of a rectangular prism is the sum of the areas of all its six faces:

\[ A = 2(lw + lh + wh) \]
This formula comes from the fact that there are:
If a rectangular prism has length 5 cm, width 3 cm, and height 4 cm, then:
\[ A = 2(5 \times 3 + 5 \times 4 + 3 \times 4) = 2(15 + 20 + 12) = 2(47) = 94 cm^2 \]
Prisms are an essential class of solid shapes in geometry. Understanding their types and surface area calculations helps in solving real-world volume and area problems. Right prisms have perpendicular sides, while oblique prisms are slanted. The rectangular prism is one of the most common forms, and its surface area can be calculated easily using a straightforward formula.