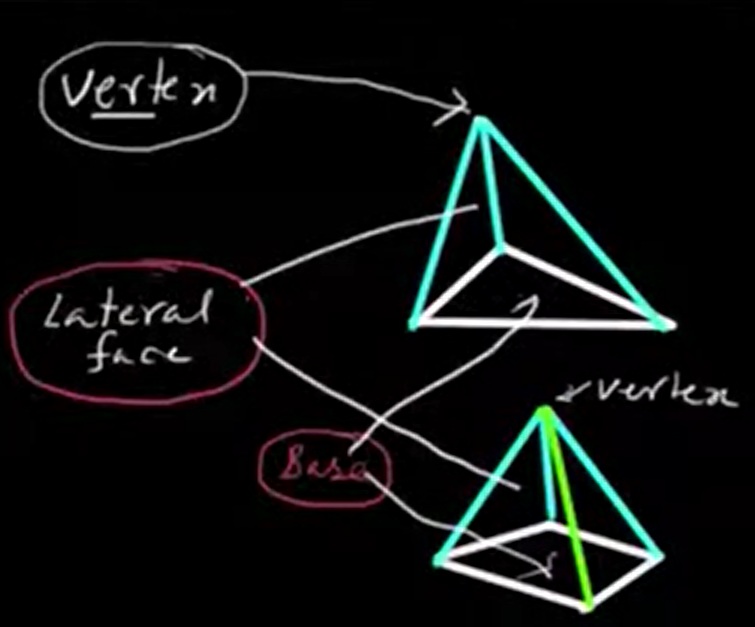
A pyramid is a three-dimensional solid figure that has a polygonal base and triangular faces (called lateral faces) that meet at a common point called the apex. The base can be any polygon — triangle, square, rectangle, pentagon, etc.
A pyramid consists of:
A regular pyramid features a base that is a regular polygon, meaning all its sides and angles are equal. The apex is aligned vertically above the center of the base, and each of its lateral faces is an identical isosceles triangle.
A right pyramid is a type of pyramid in which the apex is positioned exactly above the center of its base, so that a vertical line drawn from the apex meets the base at a right angle. It simplifies surface area and volume calculations.
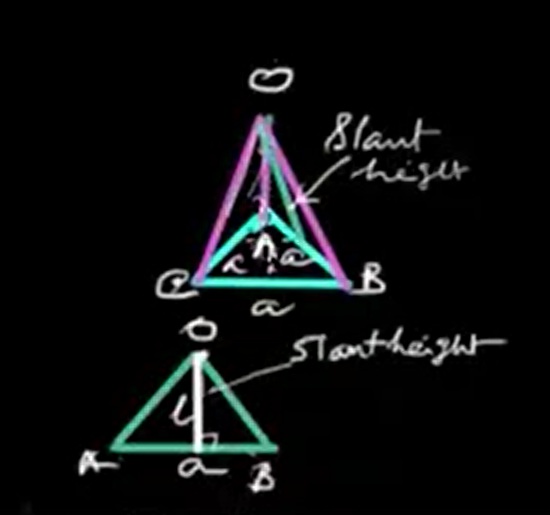
The formula for calculating the surface area \( A \) of a right pyramid is:
\[ A = B + \frac{1}{2} P l \]
Where:
The volume \( V \) of any pyramid (right or oblique) is given by:
\[ V = \frac{1}{3} \times {Base\, Area} \times Height \]
If the base is a triangle with area \( A_{base} \), and height of the pyramid is \( h \), then:
\[ V = \frac{1}{3} \times A_{base} \times h \]
To compute base area if sides are known (for triangle):
\[ A_{base} = \frac{1}{2} \times base \times height\, (of\, triangle) \]
A right triangular pyramid has a base triangle of area 24 cm² and a vertical height of 9 cm. Then:
\[ V = \frac{1}{3} \times 24 \times 9 = 72 \, {cm}^3 \]
Pyramids are fundamental 3D shapes in geometry with applications in architecture and engineering. Understanding regular and right pyramids helps in determining their surface area and volume using simple formulas.