Trigonometry | Part -4

Finding Trigonometric Ratios for Specific Angles

Trigonometric ratios such as sine, cosine, and tangent are fundamental in understanding the relationships between the sides and angles of a right triangle. Here, we explore how to find these ratios for the specific angles 0°, 30°, 45°, 60°, and 90° using the right triangle APO where angle P = 90°.

Right Triangle APO Setup

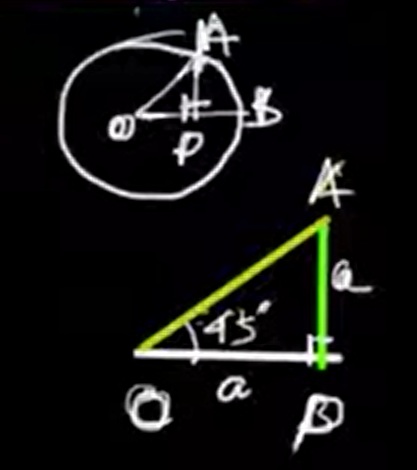
In triangle APO, angle P is the right angle (90°). The other two angles, A and O, are complementary and their sum equals 90°. The sides are labeled as follows:

• AP: The side opposite to angle O
• PO: Side opposite angle A
• AO: Hypotenuse opposite the right angle P

Trigonometric Ratios

For an angle θ within a right-angled triangle, the main trigonometric ratios include:

• Sine (sin θ): Opposite side / Hypotenuse
• Cosine (cos θ): Adjacent side / Hypotenuse
• Tangent (tan θ): Opposite side / Adjacent side

Specific Angles and Their Ratios

Explanation Using Triangle APO

Let's consider angle A as the angle θ for which we want to find the trigonometric ratios. Since angle P measures 90°, and the total sum of angles in a triangle is 180°, angle O must be equal to 90° minus θ.

- For 30° and 60°, triangle APO can be viewed as one half of an equilateral triangle with sides measuring 2 units. The hypotenuse AO is 2, the side opposite 30° (AP) is 1, and the side opposite 60° (PO) is √3.
- For 45°, triangle APO is an isosceles right triangle where AP = PO, and AO is √2 times the length of either side.
- At 0°, the angle collapses so the side opposite is 0, making sin 0° = 0 and cos 0° = 1.
- At 90°, the side opposite the angle is the same length as the hypotenuse, making sin 90° equal to 1, cos 90° equal to 0, and tan 90° undefined.

Using triangle APO with angle P = 90°, you can easily calculate the sine, cosine, and tangent values for these special angles, which are essential in trigonometry and have wide applications in science and engineering.