Types of functions | Part -1

Types of Functions: A Visual Guide Using Arrow Diagrams

Functions describe how elements from one set (called the domain) are associated with elements of another set (called the codomain). An arrow diagram provides a clear and visual method for grasping how a function works by showing arrows that link each element in the domain to its corresponding element in the codomain.

Let us consider an example to explore different types of functions using arrow diagrams:

Domain (x₁): {x, y, z}
Codomain (x₂): {a, b, c, d}

1. One-One Function (Injective)

A function is said to be one-one (or injective) if every element in the domain maps to a distinct element in the codomain. Every input from the domain is linked to a unique output in the codomain, ensuring no two inputs share the same result.

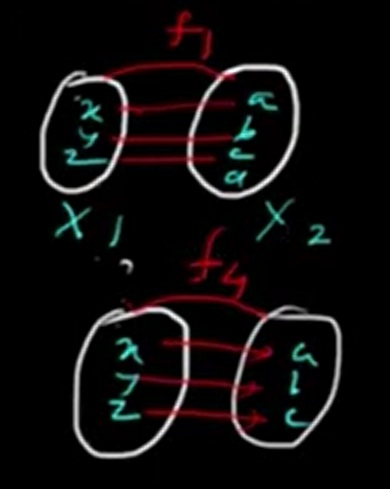
Example:
Let f₁ = {(x, a), (y, b), (z, c)}
Each element in x₁ is mapped to a unique element in x₂. Hence, f₁ is a one-one function.

Arrow Diagram: Arrows go from x → a, y → b, z → c (all unique targets in the codomain).

2. Many-One Function

A function is many-one if two or more elements of the domain map to the same element in the codomain. This remains a valid function because every element in the domain is associated with only one output in the codomain.

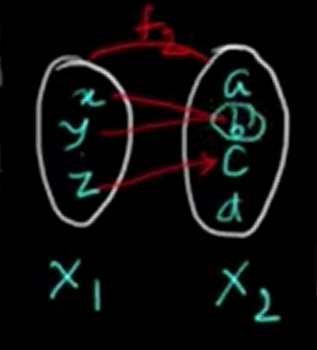
Example:
Let f₁ = {(x, a), (y, a), (z, b)}
Here, both x and y are mapped to the same codomain value 'a'. So, f₁ is a many-one function.

Arrow Diagram: Arrows from both x and y point to a; z points to b.

3. Onto Function (Surjective)

A function is called onto (or surjective) when every element of the codomain is the image of at least one element from the domain.

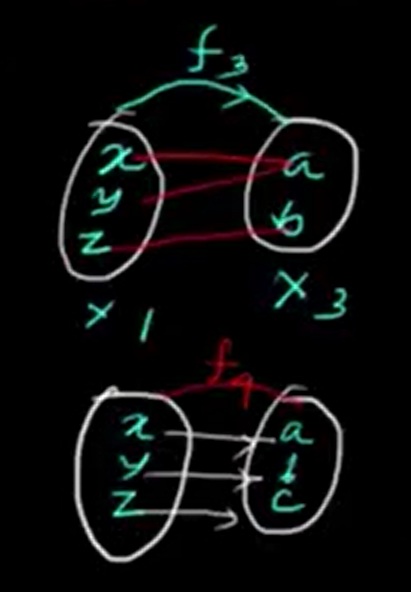
Note: Since our domain x₁ has only 3 elements and codomain x₂ has 4 elements, it is impossible to form an onto function in this particular case because at least one element in x₂ will remain unmapped.

However, consider a modified example:
Domain: {x, y, z, w}
Codomain: {a, b, c, d}
Function f₁ = {(x, a), (y, b), (z, c), (w, d)}
In this case, f₁ is an onto function because every codomain value is mapped.

Arrow Diagram: Every element in the codomain receives exactly one arrow from the domain.

In the upcoming sections, we will explore other function types like into, bijective, and constant functions with appropriate visuals and explanations.