Combination of resistance

Combination of resistance

Resistance is a key principle in understanding electrical circuits. When resistors are connected in various ways, they can form different combinations, such as series and parallel configurations. These combinations affect the overall resistance and current flow within a circuit.

Serial Resistance:

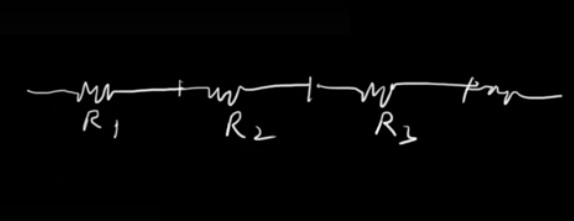
In a series circuit, resistors are arranged sequentially, creating a single route for the electric current to travel. The key feature of series resistance is that the current passing through each resistor remains the same, while the total resistance increases with the addition of more resistors. This is because the voltage across the series resistors adds up, resulting in a larger overall voltage drop.

To calculate the total resistance in a series circuit, we simply sum up the individual resistances. For instance, if we have three resistors with resistances \(R_1\), \(R_2\), and \(R_3\), the total resistance \((R_{Total})\) can be calculated as \(R_{Total}\) = \(R_1\)+\(R_2\)+\(R_3\). Additionally, Ohm's Law can be used to determine the current flowing through the circuit by dividing the total voltage \((V_{Total})\) by the total resistance \((R_{Total})\): I = \(\frac{V_Total}{ R_Total}\).

Serial resistance finds numerous applications in everyday life and electrical systems. For example, household appliances like heaters and toasters often use series resistors to control the flow of current and maintain a desired level of heat. Moreover, series resistors are used in voltage dividers, allowing the division of a voltage into smaller fractions.

Parallel Resistance:

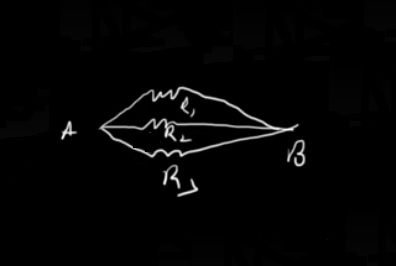
In contrast to serial resistance, parallel resistance involves connecting resistors side by side, creating multiple paths for current flow. In a parallel circuit, the voltage across each resistor is the same, while the total resistance decreases as more resistors are added. This is due to the fact that the current divides between the parallel branches, leading to an overall increase in the total current.

The total resistance in a parallel circuit is found by taking the reciprocal of the sum of the reciprocals of each individual resistance. For example, if we have three resistors with resistances \(R_1\), \(R_2\), and \(R_3\), the total resistance \((R_{Total})\) can be calculated as \(\frac{1}{R_{Total}}\) = \(\frac{1}{ R_1}+\frac{1}{ R_2}+\frac{1}{ R_3}\). Ohm’s Law helps determine the total current in a circuit by adding up all individual currents: \(I_{Total}\) = \(l_1+l_2+ l_3\).

Parallel resistance has a wide range of applications, especially in circuits where different components require different voltage levels. Household wiring, for instance, utilizes parallel resistance to ensure that various appliances receive the appropriate voltage. Additionally, parallel resistors are often used in electronic devices to divide the current, protecting sensitive components from excessive current flow.

Comparison and Conclusion:
Serial and parallel resistances possess distinct characteristics that significantly impact the behavior of electrical circuits. In summary, serial resistance increases the overall resistance while maintaining a constant current, whereas parallel resistance decreases the overall resistance while dividing the current.

Serial resistance is advantageous when a desired voltage drop needs to be achieved across each resistor, such as in voltage dividers. On the other hand, parallel resistance is useful when a specific voltage level must be maintained across multiple components.

Understanding the combination of resistance is crucial for designing and analyzing circuits in various fields, including electronics, telecommunications, and power systems. Engineers enhance circuit performance and maintain safety and efficiency in electrical systems by strategically applying series and parallel arrangements.

In conclusion, the combination of resistance, whether in series or parallel, plays a vital role in the behavior of electrical circuits. Being aware of their characteristics, calculation methods, and applications empowers us to harness the power of resistance and apply it in real-world scenarios.